Development of module-script generator for lr-mess, lr-mame and mame standalone
-
I tried this :
mame-system-adam-cart1-ui = "/opt/retropie/emulators/mame/mame -v -c adam -uimodekey TAB -cart1 %ROM%"Now the TAB works as (SCRLOCK + UI) button at the same time.
Seems quite nice, you preserve FULL keyboard emulation until TAB is pressed.Edit :
I will try that -ui_active too.
OK, that works too, nice finding !It looks like you boot in PARTIAL keyboard emulation.
Don't know if that could be a problem.We should do some more tests.
This would be nice function to add, it could make things much simpler.. -
@folly
It works also for Lr-Mess .lr-mess-system-adam-cart1 = "/home/pi/RetroPie-Setup/scriptmodules/run_mess.sh /opt/retropie/emulators/retroarch/bin/retroarch /opt/retropie/libretrocores/lr-mess/mess_libretro.so /opt/retropie/configs/coleco_sgm/retroarch.cfg \adam /home/pi/RetroPie/BIOS/mame -autoframeskip -ui_active -cart1 %ROM%" -
@folly said in Development of module-script generator for lr-mess and mame standalone:
Could be nice to add one of these functions.
Absolutely
-
Great to hear that this also works on lr-mess !
Did you try "-uimodekey TAB" too ?
What do you think? -
@folly said in Development of module-script generator for lr-mess and mame standalone:
Great to hear that this also works on lr-mess !
Did you try "-uimodekey TAB" too ?
What do you think?It changes Scroll lock for TAB. Same problem if you don't have a keyboard.
-ui_active is the best option for me. I don't see problems. Most of the time, It's already activated.
-
@folly I've tested this with mess running tic-80 games, Sega VMS, and CD-i and each game gets its own config file. I had config files already from the bezelproject for CD-i and they immediately came up as it was no longer reading tmpmess.cmd. Looks good from my testing.
-
@dteam said in Development of module-script generator for lr-mess and mame standalone:
@folly said in Development of module-script generator for lr-mess and mame standalone:
Great to hear that this also works on lr-mess !
Did you try "-uimodekey TAB" too ?
What do you think?It changes Scroll lock for TAB. Same problem if you don't have a keyboard.
-ui_active is the best option for me. I don't see problems. Most of the time, It's already activated.
Ok, good to know.
I think it's in our best interest not to make separate lines for that.
I would want to add -ui_active to the normal lines, I think that's the best option, for now.I also want to remove the separate line
mame-system-xxxxxxx-autoframeskip=.
Using 1 string we can add all options to both mame and lr-mess :mamedevcfgoptions="-v -c -autoframeskip -ui_active"This way, I only have to edit above line and we reduce some starter lines making it a bit simpler.
Good idea ?If we run into problems we can always revert it.
BTW.
Don't know if we should add this to the CMD and BASENAME lines, we could get into trouble, agreed ? -
@russellb said in Development of module-script generator for lr-mess and mame standalone:
@folly I've tested this with mess running tic-80 games, Sega VMS, and CD-i and each game gets its own config file. I had config files already from the bezelproject for CD-i and they immediately came up as it was no longer reading tmpmess.cmd. Looks good from my testing.
Super, very nice what you made 👍
Thanks for testing.
I will add this information to the first^post .
You should upvote your own idea in post 1, then we improve our ranking.😉
-
@folly said in Development of module-script generator for lr-mess and mame standalone:
Ok, good to know.
I think it's in our best interest not to make separate lines for that.
I would want to add -ui_active to the normal lines, I think that's the best option, for now.
I also want to remove the separate line mame-system-xxxxxxx-autoframeskip= .
Using 1 string we can add all options to both mame and lr-mess :
mamedevcfgoptions="-v -c -autoframeskip -ui_active"This way, I only have to edit above line and we reduce some starter lines making it a bit simpler.
Good idea ?
If we run into problems we can always revert it.
BTW.
Don't know if we should add this to the CMD and BASENAME lines, we could get into trouble, agreed ?For -ui_active I agree, but for -autoframeskip, be aware that it slowed down some systems a bit with lr-mess and MAME, but most of the time it is beneficial.
So, yes, I agree with your approach.
mamedevcfgoptions="-v -c -autoframeskip -ui_active"It's simpler for the user and he can always set buttons to set frameskip option if needed.
-
I have had a few hours re-thinking it.
Now I think it's better to do small steps, so I didn't add that much.
Editing the files, it struck me, that the "string" isn't that handy after all, so I have removed it.
That way the options are right in the lines where they suppose to be and the scripts have less lines.
I left the mame-xxxx-autoframeskip line in there, I think you have a point, when you say it doesn't always help that it is on. So I kept both lines.
With lr-mess we already had -autoframeskip in the standard line, so I left it there.https://github.com/FollyMaddy/RetroPie-Share/commit/1843471347f30fe102b3690bb0652d1af77240e4
-
Would you like to help more, in improving the scripts ?
-
I found the answers to improve the front-end script !
As I told before I now use comma separate value's within the array's.
This worked from the beginning, but there was a problem with speed.
Al the things I used before were very slow for the 38000 entry's of mame.
I couldn't usecutthat's why it took so long to find a better solution.
Now I usesedto convert the lines into csv and I use IFS to cut on delimiter and get the correct value's.
I also implemented a way of re-using the data of mame within the different menu choices. So it will read all in one time for 20 sec. and re-use this data which takes 4 sec.It now works, only the generator_script part is still old.
For that i also have to fix some things, but those are not that difficult I think.I worked from what I could accomplish, I hope it will match the direction of our ideas.
Here are some pictures :
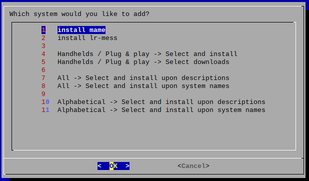
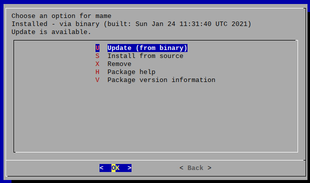
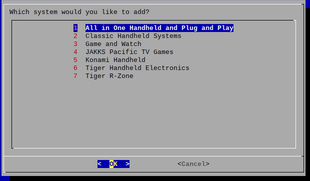
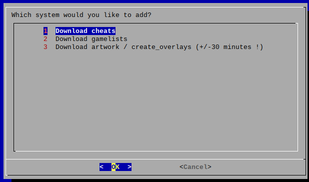
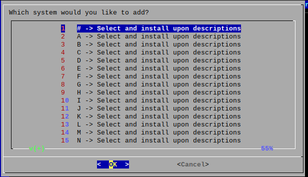
-
@folly
This is very nice!!! good work ! -
I didn't put it on github yet, there are a still a few little things to do and to check.
But I hope soon.
It's really quite amazing ! -
I moved to 2 versions of the generate-script, replacing 1v8 and 2v0:
- generate-systems-lr-mess_mame-2v1.sh generates in ~/RetroPie-Setup
- generate-systems-lr-mess_mame-2v1-ext.sh generates in ~/RetroPie-Setup/ext/RetroPie-Share
Example to generate in ~/RetroPie-Setup :
curl "https://raw.githubusercontent.com/FollyMaddy/RetroPie-Share/main/00-scripts-00/generate-systems-lr-mess_mame-2v1.sh" | bash -s colecoExample to generate in ~/RetroPie-Setup/ext/RetroPie-Share :
curl "https://raw.githubusercontent.com/FollyMaddy/RetroPie-Share/main/00-scripts-00/generate-systems-lr-mess_mame-2v1-ext.sh" | bash -s colecoOnly the
extstring is different, this defines if the files should be written in the normal directory or in the ext directory !
--> see_this_commit <--
Both files can now be pasted in as a function in add-mamedev-systems.sh front-end module-scriptEdit :
With the add-mamedev-systems-test6.sh I did the same :- add-mamedev-systems-test6.sh generates in ~/RetroPie-Setup/
- add-mamedev-systems-test6-ext.sh generates in ~/RetroPie-Setup/ext/RetroPie-Share
Get the script (in ~/RetroPie-Setup ) to generate in ~/RetroPie-Setup :
wget -q -nv -O /home/$(ls /home)/RetroPie-Setup/scriptmodules/supplementary/add-mamedev-systems.sh https://raw.githubusercontent.com/FollyMaddy/RetroPie-Share/main/00-workdir-00/add-mamedev-systems-test6.shGet the script (in ~/RetroPie-Setup ) to generate in ~/RetroPie-Setup/ext/RetroPie-Share :
wget -q -nv -O /home/$(ls /home)/RetroPie-Setup/scriptmodules/supplementary/add-mamedev-systems.sh https://raw.githubusercontent.com/FollyMaddy/RetroPie-Share/main/00-workdir-00/add-mamedev-systems-test6-ext.sh
or(only 1 version here)
You can also update the RetroPie-Share through the add-ext-repos.sh module-script.
(gets it in ~/RetroPie-Setup/ext/RetroPie-Share and generates in ~/RetroPie-Setup/ext/RetroPie-Share !)
Happy testing !
-
@DTEAM
I came across the first issue :
Sorting the descriptions is based on the system names because they are linked in one cel in the array.
That's why they are not perfectly on alphabetical order.
No solution right now, I have to think about it. -
@folly said in Development of module-script generator for lr-mess and mame standalone:
That's why they are not perfectly on alphabetical order.
No solution right now, I have to think about it.I understand what you mean. The numerical order go in front of alphabetical order. You are not far to the end of the project !! Have you think about a way to separate MESS systems from global MAME list? Bye the way, It's awsome!
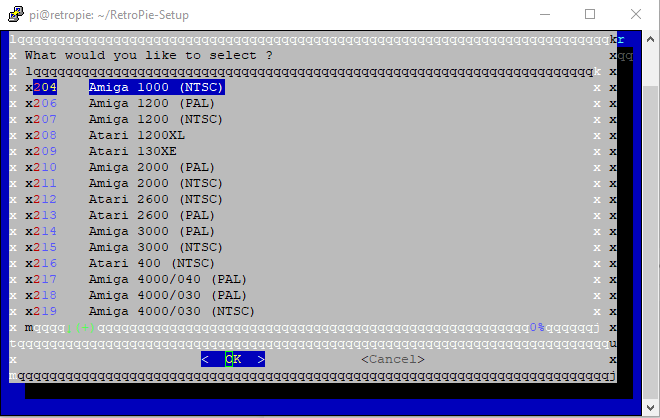
-
@dteam said in Development of module-script generator for lr-mess and mame standalone:
@folly said in Development of module-script generator for lr-mess and mame standalone:
That's why they are not perfectly on alphabetical order.
No solution right now, I have to think about it.I understand what you mean. The numerical order go in front of alphabetical order.
Well, it's not exactly that.
But you are in the right direction.You are not far to the end of the project !!
Indeed it progressing nicely !
Have you think about a way to separate MESS systems from global MAME list?
Yes I have been thinking about that.
I was looking at the mame source, arcade drivers are in a different place than the machine drivers.
But, for now, I have no idea on how to accomplish that.
Within minutes the structure can be quite difficult to understand.
And I have to take speed into account too.
That make this quite hard.I was also thinking of making entry's by platform.
I think that can easier be done, just like the A,B,C story.If I have some spirit I will look at those issues.
Bye the way, It's awsome!
Thanks for the compliment !
It is ! Really unbelievable ;-) -
@folly I'd love to.
Here's a question, probably for a new thread. I installed a PixelCade LED marquee in my bartop arcade build which requires a customized EmulationStation that calls web services on the local machine which has a listener to interact with the marquee. I didn't like having to specifically modify ES for this purpose so I implemented three new events: game-select, system-select, screensaver-game-select, and moved the logic to bash scripts. I've seen other threads that discuss wanting this capability. Is that something users would like?
-
@russellb said in Development of module-script generator for lr-mess and mame standalone:
@folly I'd love to.
Great !
Contributions to the project are always appreciated, so if you would like to support us with a donation you can do so here.
Hosting provided by Mythic-Beasts. See the Hosting Information page for more information.