Better than CRT quality?
-
@fishermanbill said in Better than CRT quality?:
So how might we get "a better than CRT" image on a LCD/OLED screen without using all those high cost, blurry, moire pattern ridden shaders that come with Retroarch/libretro? That's a bit harsh I know some of them are technically excellent - I'm just not a fan of them visually.
moire patterns are resolved if you run at a high enough resolution (more pixels per scanline), and also can be virtually invisible on a 1080p display IF it is configured correctly (ie, running it in full panel resolution - https://retropie.org.uk/docs/Overscan/#my-image-is-cut-off). it's tricky with vertical games as they use such a small portion of the screen, so even less pixel density to work with, but check out https://retropie.org.uk/forum/topic/4046/crt-pi-shader-users-reduce-scaling-artifacts-with-these-configs-in-lr-mame2003-lr-fbalpha-lr-nestopia-and-more-to-come
Well let's set out one definite feature of a CRT we want to emulate and that's the scanlines! I believe these are fundamental to the retro gaming look.
We also want to aim for crisp pixels and no moire patterns so we always need integer scaling.i don't neccesarily agree with this because many systems/games did not use 1:1 PAR. eg, if you use integer scaling with Street Fighter II (arcade) it will be in a widescreen type mode, making all the characters 'fat'. but yeah it can give good results for sure, if you're careful with games that don't have 1:1 PAR.
This brings up a thorny issue - that of screen resolution. Retropie as far as I can tell can only really output a 1080p image - 4K is technically possible but the refresh rate takes a hit as the underlying hardware is just not powerful enough or hasn't been optimised for
you can run retropie on an x86 pc, or faster SBC, etc.
This will almost always use some sort of bilinear/trilinear etc filter
not sure what you mean by this? a 4k screen should render a 1080p image crisply with no scaling artefacts, since 1920x1080 (1080p) x 2 is 3840x2160 (4k) - again you will need to ensure you're on the right display mode to ensure it's using every pixel of the panel.
I’ve found there is a bug with Mame2003, vertical arcade games, integer scaling and custom viewports. Basically it tells Retroarch/EmulationStation the wrong width and height when rotated i.e you're viewing a game on a landscape oriented screen. This results in an incorrect aspect ratio and breaks this shader badly but it also breaks all other shaders and its just wrong.
i'm not quite sure what you mean by this. i have some experience with vertical games + shaders + mame2003 but i'm not aware of this bug.
(sorry for the pedantry and avoiding the substance of the post, just aspect ratios are my passion, lol.-the shader/discussion is cool!)
-
Thanks for your reply! I suppose I should have made clear in my original post that I did tailor it to RetroPie as in outputting 1080p to various screens as I think the RetroPie is an ideal device for retro gaming largely because of its size. Sure you can use a PC to directly output to different screen resolutions but I probably would have posted to the LibRetro forum for that type of stuff. In any case the approach I want to use here still has the same problems of screen brightness on PC.
So as for moire patterns ok you may not percieve them in certain scenarios but the underlying problem still exists of uneven or blurry scanlines and as long as that exists you have the potential to witness moire patterns.
Of course all the standard shaders of libretro deal with the problem by either having uneven scanlines or just blurring them. Thats fine if you like that sort of thing I personally dont and as you touch on, the problem gets worse when you go down to lower res screens as in Pimoroni's Picade with its 1024x768 screen. Also seeing all the screen on CRT's was never a thing - there was always some part of the screen chopped off - so in a way using an 'overscan' resolution is more accurate but yes integer overscaning does cut off more of the screen than most TV's back then.
Essentially I want to solve this problem by instead using integer scaling and precise pixel scanlines and by default libRetro (and therefore eveything based on it) doesn't really provide an option out of the box for this approach - at least not a shader. Also its custom viewport support seems buggy - at least in RetroPie's 4.7.1 (I'll come back to this below).
As for Street Fighter II yes I'm aware of the fat character problem and the reason for 1:1 PAR. So yes in the purist approach of my post you would have to accept fat characters. However as you know aspect ratio is a ratio between the width and height and so you can still have integer scaling in the all important y axis whilst maintaining crisp scanlines and then have a non integer scaling in the x axis to have a PAR aspect ratio and make the characters look 'normal' or whatever that was for the screen you were looking at it on. Sadly I'm not sure Retroarchs interface (or supported interface at least) makes that easy to do - it is possible though.
"a 4k screen should render a 1080p image crisply with no scaling artefacts, since 1920x1080 (1080p) x 2 is 3840x2160 (4k)"
You would expect that but no TV/monitor on the market will do that - if you input a 1080p signal it will use the bilinear/trilinear/smart etc blur filter ('smart' being an adaptive blur filter) to upscale it to 4K not a nearest neighbour filter. This is because for normal footage (its arguable) thats better but for pixel art its not. Some Panasonic screens I believe had a 'game mode' that would directly scale it as you say i.e 1 pixel upscaled directly to a 2x2 pixel quad. However I believe those models were discontinued. Eve's Spectrum is the first monitor on the market to provide an integer upscale.
Let me get some more information for you on mame2003 + vertical arcade + custom viewport + integer scaling bug. It maybe an out of date Retroarch/mame2003 or I maybe am using a different core to what I thought. Its definitely a bug on the version of RetroPie I have - I'll take some screen shots to show you.
-
@fishermanbill said in Better than CRT quality?:
Thanks for your reply! I suppose I should have made clear in my original post that I did tailor it to RetroPie as in outputting 1080p to various screens as I think the RetroPie is an ideal device for retro gaming largely because of its size.
what i mean is 'retropie' does not mean 'raspberry pi' - it's an emulator setup script that can be installed on many devices, including PC. i think you mean 'retropie on raspberry pi' :) (pedantic i know...)
Of course all the standard shaders of libretro deal with the problem by either having uneven scanlines or just blurring them. Thats fine if you like that sort of thing I personally dont and as you touch on, the problem gets worse when you go down to lower res screens as in Pimoroni's Picade with its 1024x768 screen.
the general rule is that a scanline shader needs 4 vertical rows of pixels for every scanline. on a typical 320x240 game that would be 240*4=960, so a 1080p screen should generally give you good results with no obvious blurring, but 768 will be a very bad time and demand integer scaling (and the ensuing borders/overscan).
but... if you use an integer scale on those scanline shaders there should be no blurring.
Also seeing all the screen on CRT's was never a thing - there was always some part of the screen chopped off - so in a way using an 'overscan' resolution is more accurate but yes integer overscaning does cut off more of the screen than most TV's back then.
for home consoles this is true, but there is a certain amount of overscan that is expected for such systems - there is normally no game-critical information rendered in those portions, as you can't guarantee that a given home CRT is going to display it. conversely, some games actually hid necessary garbage in those areas on the presumption that 99% of sets wouldn't show it - eg mario 3's extreme horizontal edges.
so, yes having some overscan is accurate for home consoles, but only within those specific screen regions.
...but arcade machines are different. these were not consumer CRTs and arcade machines where configured by technicians/arcade owners per-game. these games regularly use the whole of the 240p (or whatever) image. for example, see how the score is right at the top of the screen, and the bombs right at the bottom in donpachi:

However as you know aspect ratio is a ratio between the width and height and so you can still have integer scaling in the all important y axis whilst maintaining crisp scanlines and then have a non integer scaling in the x axis to have a PAR aspect ratio and make the characters look 'normal' or whatever that was for the screen you were looking at it on. Sadly I'm not sure Retroarchs interface (or supported interface at least) makes that easy to do - it is possible though.
yeah, you can do this, although that will inevitably cause borders/overscan depending on whether you want to run under/over. i did actually experiment with this approach using the scripts i linked previously, but i found it not worth it.
but it does require some calculations. in the SF2 example, if you use integer scaling on Y, and leave X at non-integer, you're still going to end up distorting the image unless you adjust X, because the aspect ratio is going to change. what you'd need to do is adjust X accordingly. eg, for SF2 at 5x Y, that's 5x224=1120. the X is 1440 by default (ie, it's a 4:3 game so if Y is 1080, then X is 1440), so to maintain 4:3 for a 1120 Y we'd have to change X to 1493(.333). it won't automatically do this, but a script like the one i linked before could do these calculations for you, with adjustment.
also, you can do this manually do this via the RGUI: when you select custom resolution it tells you when you're at an integer scale as you adjust the resolution (see "4x"):
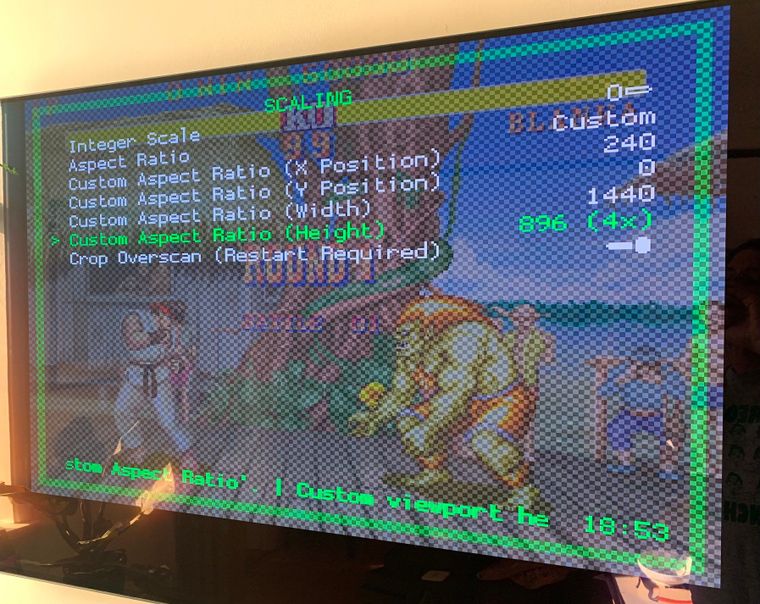
but yeah you'd still need to adjust X as per a calculation.
"a 4k screen should render a 1080p image crisply with no scaling artefacts, since 1920x1080 (1080p) x 2 is 3840x2160 (4k)"*
You would expect that but no TV/monitor on the market will do that - if you input a 1080p signal it will use the bilinear/trilinear/smart etc blur filter ('smart' being an adaptive blur filter) to upscale it to 4K not a nearest neighbour filter. This is because for normal footage (its arguable) thats better but for pixel art its not.
i have not experienced this with my 4k TV at 1080p - an LG OLED, but you do have to correctly configure it, as i've said. here's some proof - a close up shot of the console at 1080p:
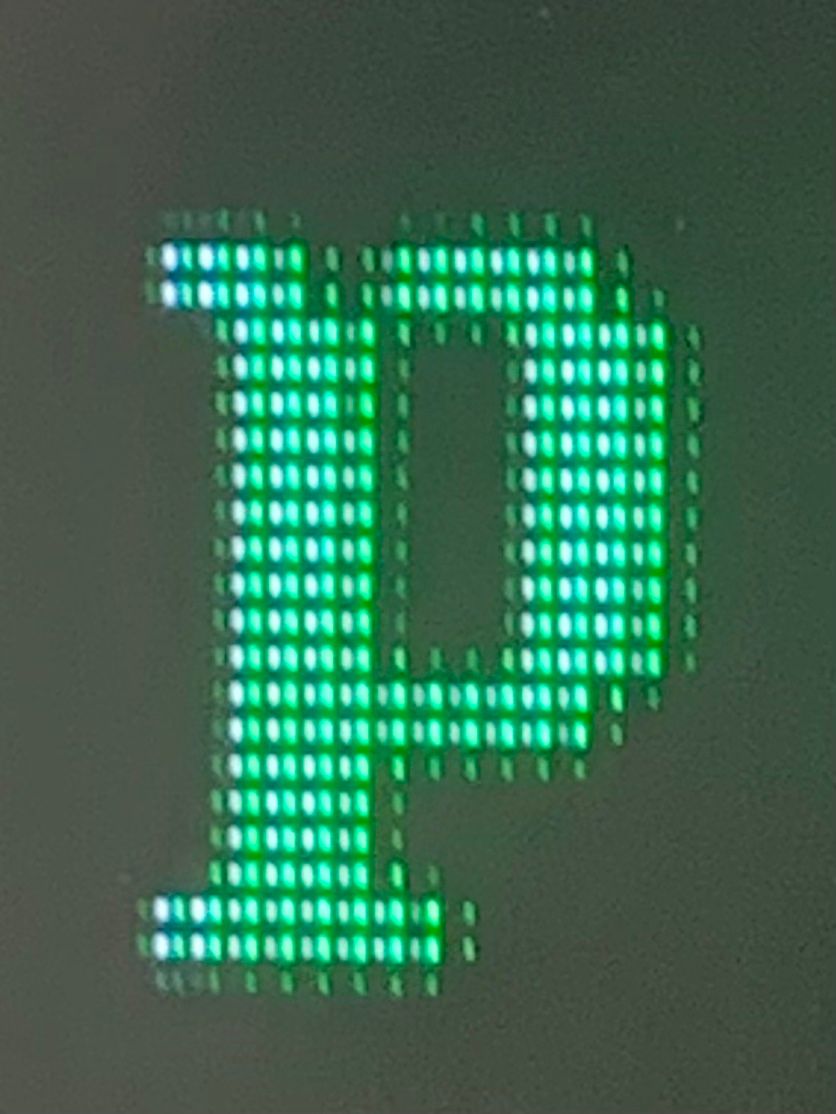
the linux console, by default, has a font made up of lines 1-2 pixel 'thick'. there's no bilinear filtering or font smoothing. as you can see, this becomes 2x2 squares on my screen. forgive the light bleed - this is with some glare from the sun, but the light is only being emitted from those OLED diodes, with no scaling/smoothing beyond that basic 1x1=2x2 transformation.
i would be very surprised if this configuration is not possible for all major TV brands - we have instructions for Samsung, LG and Pioneer here: https://retropie.org.uk/docs/Overscan/#my-image-is-cut-off (please ignore that this is the overscan doc - this also fixes an overscan issue but what these tweaks effectively do is make sure an HD/4k source image is displayed 1:1 on HD/4k tvs).
-
@dankcushions
I'm pretty sure your big image of the 'P' is showing exactly what I'm saying i.e its not mapping one pixel directly to a 2x2 pixel quad with no adjustments. As in the 'P' is surrounded by a one pixel pattern - that wouldn't be possible on a pure nearest neighbour upscale right? You can argue its light bleed but then you have to ask how the TV knows it displaying pixel artwork and shouldnt be upscaling it with a blur filter as all other media would want that including high end consoles. If its guessing then its going to get it wrong at some point.I'll have a look at your scripts as it may help to automate things for me - thanks!
So in my opinion 4 or 5 pixels is not enough to provide a decent representation of a scanline surrounded by black inlcuding a faux bloom effect. As in you now have only two or three pixels to contain the blurred edge. Its just too low a resolution for what people want to do and this really gets to the heart of my original post: why bother blurring the edge of the scanlines to mimic the high brightness of a CRT when we can probably now just use the HDR brightness of modern monitor/TV sets to actually create a real bloom ourselves.
As for the 5x overscan approach this is pretty much the standard on the MiSTer platform and what most people recommend over there for LCD's. In fact last year the lead developer added support for overscaning and integer scaling support like this to all the cores for this very reason. However its up to you whether you like this approach vs others there always swings and roundabouts with this.
I would have thought most people on the RetroPie forum would be using a RetroPie image on a Raspberry Pi but then again maybe I'm missing something and this is actually an EmulationStation on Raspberry Pi forum.
-
@fishermanbill
Yes thats definitely not light bleed on the 'P's one pixel pattern edge - you can see on the right hand side the one pixel pattern has a gap of dark sub pixels and then one light sub pixel that wouldn't happen if it was light bleed. They are also the same luminosity on both sides - left and right. Its difficult to say for certain but I'd guess those pixels are being turned on by your TV. -
@fishermanbill i have to apologise - i tried it in native 4k and didn't have that light bleed (i should have trusted OLED tech better!), so clearly there was something up, but i found the setting - super resolution - it adds detail to sub-4k images - ie antialiasing. this was enabled by default, even in game mode - by turning it off i have pixel perfect fonts:

I would have thought most people on the RetroPie forum would be using a RetroPie image on a Raspberry Pi but then again maybe I'm missing something and this is actually an EmulationStation on Raspberry Pi forum.
most people, yes, but i was just making the point that retropie on pc (or odroid or whatever) is still "retropie" :)
-
@dankcushions
No need to apologise at all, this is a learning process for all of us and I didn't know an option existed on the LG OLEDs for such a thing. Very interesting. So you couldn't do me a favour and see how good support it has for integer scaling? As in, is it only from 1080p to 4K that it does it? Also something else looks to be going on with the top of the 'y' and possibly the bottom of the back stroke of the 'y' - local dimming maybe (hmm actually no as its an OLED), just the effect of the camera? To be honest thats a minor nitpick if the image is being scaled correctly for pixel art with a nearest neighbour filter.I believe the Eve's Spectrum monitor alllows complete control of the image like RetroArch does in that it will allow you to take in a lower image resolutions (not just 1080p) and integer scale it up beyond the screen size and then move it around with an offset. However I've yet to see anybody who's got one show that functionality. Potentially this could offload work from the Pi to the monitor and allow the Pi to run cooler and or faster with overclocking. Mind you at that point you could argue just to get a more powerful computer than a more costly monitor but then its the image quality.
Going back to my original post and brightness I'm not sure an OLED is going to be bright enough to get up to high end CRT brightness levels. I think the LG OLED C1 has about ~350cd/m2 and I think we'd need to be double that to get a nice natural bloom effect - I could be wrong. Possibly the Samsung QLED TV's might be able to achieve it but then I'm not sure that the back light LED's are small enough not to cause light bleed.
-
@dankcushions said in Better than CRT quality?:
super resolution
Ah I've just looked into 'LG's Super Resolution' and its not a nearest neighbour upscaler. Although its done a good job of your test above, as in what we would like for pixel art, I don't think it would do the same job in all/majority of cases. I think as soon as you bring in colour and motion, it'll do all sort of things as its a 'smart' upscaler as I mentioned in my original post. It'd be interesting to see some tests to prove that theory out but the 'y' in the picture above starts to hint at that kind of thing going on.
-
@fishermanbill to be clear super resolution is turned OFF in my photo. it’s the upscaler that adds fidelity when upscaling from sub-4k, when in our case we don’t want that, so i turned it off. in the absence of that it appears to do a simple 1x1=2x2 transform.
-
Ah sorry missed read that - that makes more sense - ok good so it is doing nearest neighbour!
Contributions to the project are always appreciated, so if you would like to support us with a donation you can do so here.
Hosting provided by Mythic-Beasts. See the Hosting Information page for more information.